What You’ll Learn in This Post

1. How to plot temperature, dewpoint, and wind observations on a Stüve diagram
2. How a skew-T diagram is different from a Stüve diagram
3. How a skew-T diagram can be used in different applications
4. How to download a skew-T diagram from the internet

Introduction

To forecast the weather, meteorologists rely on data collected directly from the atmosphere. We collect this data by launching weather balloons, usually twice per day. These weather balloon observations, called “soundings” and often plotted as skew-T log-p diagrams, give meteorologists direct evidence of the current weather conditions at different heights in the atmosphere. This is important because most of the weather happens above the ground, while we live on the surface.

A Simple Graph of Pressure vs. Height: The Stüve Diagram

The graph below contains data from Blacksburg, VA (station abbreviation: RNK). The balloon was launched at approximately 1200 Universal Time Coordinate (UTC time) on May 3, 2022. UTC time (or “Zulu” time) is based in Greenwich, England and does not observe Daylight Savings Time. You’ll know the time of the sounding from the bold black number (12Z) next to the date at the lower left on the graph below.

It can be challenging to graph these data, because the atmosphere is heated from the surface upward and tends to get increasingly colder with increasing height. As you can see in the image below, the graph is highly tipped over, representing a strong decline in temperature with height.

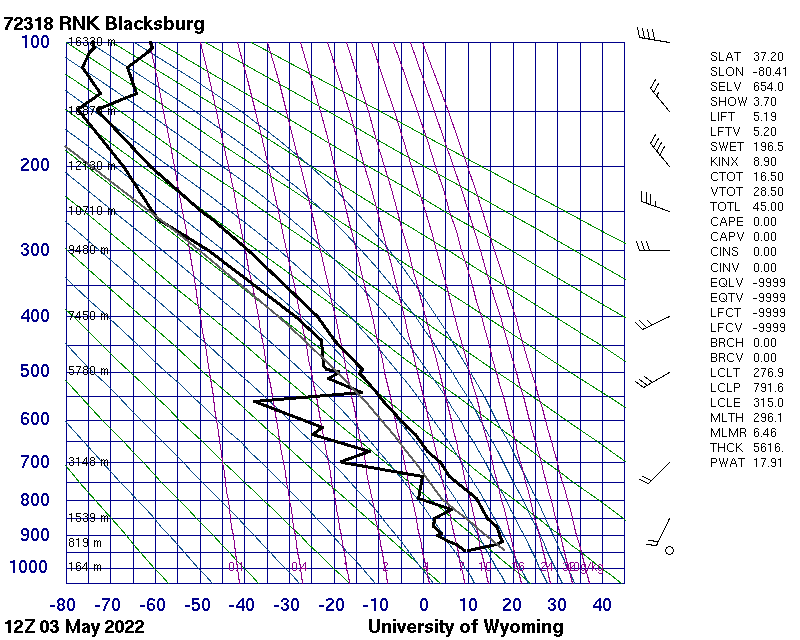
The graph above is called a Stüve diagram. It shows the temperature (x-axis) versus the pressure (y-axis). Two temperatures are plotted: the air temperature (right bold line) and the dewpoint temperature (left bold line). The dewpoint temperature is shown to represent moisture in the atmosphere. Meteorologists often use pressure, rather than height, as the vertical coordinate. The pressure is shown by the blue numbers at the left of the graph, which decrease with height. This decrease occurs because at higher elevations, there are fewer molecules above to “weigh down” from above onto a given level. Notice that the pressure lines spread out higher in the graph. This is because pressure decreases exponentially with height, so the values decrease at a slower rate higher in the atmosphere.

Just to the right of the blue pressure numbers are smaller black numbers showing the height in meters. Along the bottom of the graph, the blue numbers show the temperature in degrees Celsius. Just to the right of the graph are symbols indicating the wind speed and direction. The circle at the bottom of that column indicates calm winds (or a lack of wind). Finally, the numbers at the far right show various computed quantities from the data.

The Skew-T Diagram

We have a problem: anytime we try to plot temperature versus height in the atmosphere, the graph will tip over dramatically to the left. Can we tilt the data to be more upright?

Below is a basic image of a “skew-T” diagram without any data plotted. It shows the height on the y-axis and temperature on the x-axis. Notice that the height scale in kilometers is the same on the left and to the right of the plot. Heights in thousands of feet are also shown on the right. Notice the diagonal lines from lower left to upper right: that’s our new, tipped-over temperature axis. It’s called a “skew-T” because the temperature axis is “skewed”, or slanted at a 45-degree angle. This will allow the temperature and dewpoint temperature data to be more upright when plotted than on the Stüve diagram above.

The graph below might give you a better sense of scale. On the left, pressure is plotted instead of height. Notice that the diagonal temperature lines are evenly spaced, and that the horizontal pressure lines spread out with increasing height. A skew-T is technically called a “skew-T log-p” diagram because the pressure numbers are logarithmic. But we’ll keep it simple and refer to them as skew-T diagrams.

Finally, the plot below shows how the freezing line (diagonal black line) is slanted in our new skew-T diagram, like all temperature lines (known as isotherms). In the red region, the air is above freezing. In the blue region, the air is below freezing.

Now let’s plot the same data as in the first image in this post on a skew-T diagram, and we’ll highlight where the weather balloon noted important data points with circles. On the skew-T below, we also plot a colorful vertical ribbon showing the wind speed. There is much more detail in the wind data at the right of this graph than in the Stüve diagram that started this post.

Comparing the Stüve and Skew-T Diagrams

Here’s a side-by-side comparison of this skew-T we just plotted (left) and the original Stüve diagram (right) from the beginning of this post. Notice that the skew-T brings the temperature data more upright, but exaggerates the differences between the air temperature and the dewpoint temperature.

We’ll add one more wrinkle to the mix, by plotting a graph of the wind speed (blue line) to the right, between our temperature data and the wind data. Notice that the colors in the vertical wind speed ribbon correspond exactly to the changes in the wind speed on the wind speed graph because we are plotting the same variable.

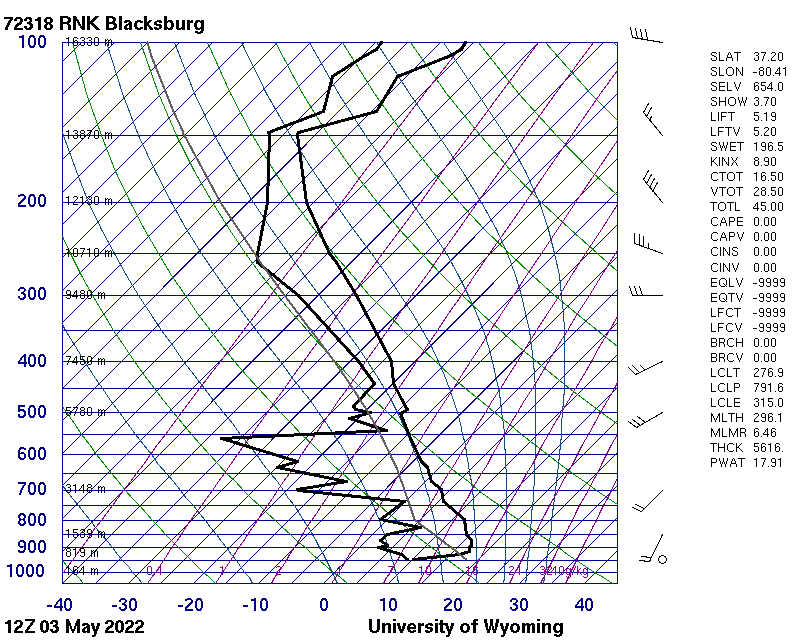
Finally, we have below the skew-T generated by the University of Wyoming sounding website for the same station and time as the Stüve diagram that started this post. This diagram has some extra background lines that are used in interpreting the stability (and, therefore, the potential for vertical motion) within the atmosphere. The temperature axis is indicated by the blue lines slanting upward and to the right at a 45 degree angle. You can go to the Univ. of Wyoming link above and play around to your heart’s content…but if you want a skew-T, be sure to change the “Output Type” to PNG: Skew-T.

Please wait…

1. Where is the pressure axis on a skew-T diagram?

Along the horizontal axis

Slanted at 45 degrees to the horizontal axis

To the right of the main graph

Along the vertical axis

Question 1 of 7

2. Where is the temperature axis on a skew-T diagram?

To the right of the main graph

Along the horizontal axis

Along the vertical axis

Slanted at 45 degrees to the horizontal axis

Question 2 of 7

3. What does the circle in the winds column of a skew-T diagram indicate?

Problem with the wind sensor at that level

Calm winds

No wind data at that level

Question 3 of 7

4. Why is the freezing line slanted on a skew-T diagram?

The temperature axis is slanted on a skew-T diagram

The freezing point of water changes significantly from the surface to higher levels in the atmosphere

Question 4 of 7

5. Why do the pressure values get farther apart higher in the atmosphere?

Pressure decreases more slowly with increasing height

Pressure decreases more rapidly with increasing height

The atmosphere is warmer at higher altitudes

The atmosphere is colder at higher altitudes

Question 5 of 7

6. Which data line is the temperature line on a skew-T diagram?

The bold line on the right

The bold line on the left

Question 6 of 7

7. Where are the winds indicated on a skew-T diagram?

To the right of the main graph

Slanted at 45 degrees to the horizontal axis

Along the horizontal axis

Along the vertical axis

Question 7 of 7

 Loading…

 

In the next installment, we’ll apply our knowledge of skew-T diagrams via an example that compares a skew-T plot to a video of some clouds around the same time.